Simplificación de circuitos lógicos

Nuestra tarea es simplificar un diagrama de compuertas lógicas:

Las instrucciones dicen:

• Simular este diagrama
• Obtener ecuación [lógica] original
• Simplificar la ecuación
• Armar [en físico] el circuito de la ecuación simplificada
• Comparar el funcionamiento [del circuito armado con el simulado]

Haremos todo el proceso con el fin de demostrar la utilidad de las simplificaciones lógicas.

Para simular este circuito en computadora, utilizaremos el programa MultiSim 11.0, de National Instruments.

Este diagrama representa la base de un circuito para conectar compuertas lógicas. Nótese que tiene un LED que sirve de indicador para saber si la señal de salida final fue 1 o 0. Si deseas usar esta plantilla para tus propósitos, puedes usar la imagen como guía o bien descargar el archivo de Multisim, presionando aquí.

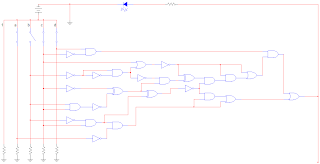
Primeramente, tenemos el diagrama ya armado por computadora, tal y como lo entendimos. Puedes descargar el archivo para Multisim presionando aquí.

Esta es la (larguísima) fórmula que obtuvimos. Es álgebra booleana. Clic para agrandar

Aplicando leyes del álgebra booleana (teorema de Morgan y otras), podemos simplificar fórmulas como ésta. Siempre hay una explicación para el comportamiento del álgebra booleana, pero para ahorrarnos explicaciones, enlistaremos unas cuantas leyes comprobadas, que siempre se cumplen. De momento no explicaremos cómo funcionan.
Algunas de las leyes que nos enseñaron en el salón de clases, para compuertas de 2 entradas (debido a las limitaciones de este medio, las negaciones no van con una raya arriba, sino tachadas):

• aa = a
• aa = 0
• a0 = 0
• a1 = a
• a+a = a
• a+a = 1
• a+0 = a
• a+1 = 1
• (a+b) = (a)(b)
• (ab) = (a)+(b)
• a [negada dos veces] = a [sin negar]
• a xor b = ab+ab

He aquí la tabla de verdad y su comprobación: 

• 0000  -  0
• 0001  -  1
• 0010  -  1
• 0100  -  1
• 0100  -  0
• 0101  -  1
• 0110  -  0
• 0111  -  0
• 1000  -  0
• 1001  -  1
• 1010  -  0
• 1011  -  0
• 1100  -  0
• 1101  -  1
• 1110  -  0
• 1111  -  0

Después de aplicar las leyes booleanas e incluso indagar e investigar un buen rato sobre este tema, hemos reducido la fórmula a una mucho más elegante, simple y legible. Por el momento desconocemos si se pueda simplificar aún más (en cuyo caso nos encantaría que nos lo hicieran saber). Aquí va la fórmula simplificada:

Creemos que esta fórmula es equivalente a la anterior ya que la tabla de verdades resultante es la misma. Pueden descargar el archivo de MultiSim para el circuito simplificado, haciendo clic aquí.

• 0000  -  0
• 0001  -  1
• 0010  -  1
• 0100  -  1
• 0100  -  0
• 0101  -  1
• 0110  -  0
• 0111  -  0
• 1000  -  0
• 1001  -  1
• 1010  -  0
• 1011  -  0
• 1100  -  0
• 1101  -  1
• 1110  -  0
• 1111  -  0

Muy bien, ahora lo único que queda es armar el circuito...No disponemos de compuertas AND de 3 entradas, por lo que tendremos que usar un pequeño truco para adaptarlo a las compuertas que tenemos (y que también tiene su explicación lógica): Las dos primeras entradas irán a la compuerta AND A; y tanto la última entrada como la salida de la compuerta A, irán a la compuerta B. Así:

Y el circuito quedaría de esta manera:

Ahora, pasemos a armarlo. Primero armamos el circuito base para compuertas lógicas:


Lista de materiales:

• Proto-Board
• Cables para puentear
• Circuito integrado HD74LS04P
• Circuito integrado HD74LS08P
• Circuito integrado HD74LS32P
• DIP switch que tenga por lo menos 4 entradas
• 2 resistencias de 1KΩ
• 1 resistencia de 330Ω
• 1 LED
• 1 fuente de 5V de corriente directa
  (éste es el voltaje recomendado por las datasheets de los circuitos integrados)

Los circuitos integrados son (en el orden de izquierda a derecha, como se ven en la imagen) compuertas OR, AND y NOT

Después, conectamos las compuertas para armar nuestro circuito. Aquí están cada una de sus entradas y salidas:
Cuando cada switch respectivo está hacia la posición de "ON", la entrada de la compuerta es un 1. El switch #1 es para la entrada a, el #2 es para la b, el #3 para la c y el #4 para la d. El led encendido indica salida 1, y cuando está apagado indica salida 0.

Fuentes consultadas:

• Información vista en clase
• Artículo sobre álgebra booleana que no recuerdo