Deseamos construir un circuito lógico que haga lo siguiente:
En un automóvil, encender una alarma si el motor está encendido y hay algún pasajero sin el cinturón de seguridad abrochado.
Supondremos que hay 5 lugares para sentarse en el automóvil. Cada lugar tiene un mecanismo que detecta si hay alguien sentado ahí, y otro mecanismo que detecta si el cinturón está abrochado.
Asimismo, hay un mecanismo que detecta si el motor está encendido.
Todos estos mecanismos enviarán una señal de salida con una respuesta positiva o negativa según sea el caso. La respuesta positiva será una señal 1 y la negativa será una señal 0.
Yo construí una ecuación lógica de este problema, pero la presentaré hasta el final, con el propósito de presentar y desarrollar la cadena de razonamientos que me llevaron a ella. Empezaremos por el final:
¡Hemos terminado nuestra lógica de seguridad! Así queda el circuito completo y simulado:
Le queremos sacar su tabla de verdades, pero serían 212, es decir, 4096 salidas posibles, así que lo más factible es dividir el circuito en partes más manejables y prácticas.
¿Los resultados tienen sentido? ¿Sí? ¡Muy bien! Ahora lo simularemos en físico. Veamos cómo hicimos esta práctica:
Yo construí una ecuación lógica de este problema, pero la presentaré hasta el final, con el propósito de presentar y desarrollar la cadena de razonamientos que me llevaron a ella. Empezaremos por el final:
 |
| Para que se active la alarma, se tienen que cumplir dos condiciones: que el motor esté encendido y que haya inseguridad en los asientos. Esto último se decidirá en base a los pasajeros con cinturón desabrochado. La entrada que indica si el motor está encendido es bastante simple...Sólo puede entrar 1 ó 0. Esta entrada va conectada directamente al sensor que nos permite saber si el motor está encendido, así que aquí acaba la parte del motor. La entrada que indica si hay inseguridad en los asientos tiene más cosas detrás...Tiene más historia. A continuación veremos el flujo de valores lógicos y compuertas lógicas que conforman este valor. El nodo está marcado en amarillo. |
 |
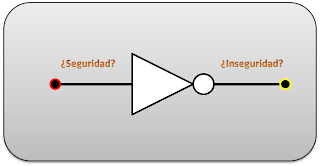| Para saber si hay inseguridad, primero deberemos saber si hay seguridad, y luego invertiremos el resultado con una compuerta NOT. ¿Cómo sabemos si hay seguridad? Veremos qué hay detrás del nodo rojo. |
 |
| Para que haya seguridad en general, todos y cada uno de los 5 asientos, sin excepción, tienen que estar seguros. Ahora bien, todos los asientos se toman como iguales y usan la misma lógica. Veamos qué hay detrás de un nodo azul. |
 |
| Para que un asiento se considere seguro, se necesita cumplir una de las siguientes condiciones: Que ell asiento esté desocupado (con lo cual será irrelevante si el cinturón está abrochado o no) o bien si hay un pasajero que el cinturón forzosamente esté abrochado. La entrada que tiene que ver con el cinturón está directamente conectada, sin compuertas lógicas por detrás. Pero espera, observa que la pregunta "¿NO hay pasajero?" contiene una negación. Veamos qué hay detrás de ella (nodo verde) |
 |
| Para poder responder si NO hay un pasajero, primero respondemos si SÍ hay un pasajero. Esta entrada va conectada directamente al sensor de pasajeros a bordo. |
¡Hemos terminado nuestra lógica de seguridad! Así queda el circuito completo y simulado:
 |
| Así queda la ecuación lógica |
 |
| Esta es una de tantas posibles representaciones del circuito lógico, hecha en el programa MultiSim 11. No tuvimos disponibles compuertas AND de 5 entradas (ni en el programa ni en físico), por lo cual hicimos un juego de compuertas AND de 2 entradas, para conseguir el mismo efecto. El archivo de la simulación en MultiSim lo puedes descargar presionando aquí. |
 | |||||||||||||||
Esta parte del circuito representa cada uno de los asientos.
|
 |
| La salida de cada asiento es la entrada a este AND de 5 entradas. En realidad no necesitamos tomarnos la molestia de sacar una tabla de verdades puesto que el único caso en el que la salida será 1 será cuando todas las entradas sean 1. |
 |
| La salida negada del AND de 5 entradas (B) es una de las entradas del AND final, y la otra (A) es el encendido del motor. |
a
|
b
|
x
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
¿Los resultados tienen sentido? ¿Sí? ¡Muy bien! Ahora lo simularemos en físico. Veamos cómo hicimos esta práctica:
 |
| Puesto que necesitamos 11 entradas para para este circuito lógico, hemos tenido que utilizar varios DIP switches. En este caso, utilizamos uno de 8 entradas y otro de 4 entradas. Al final de cada uno, hemos utilizado una resistencia de 1KΩ. La fuente fue de 5V DC. |
 |
| Si, para el circuito con compuertas lógicas, utilizásemos los mismos circuitos integrados que hemos utilizado en prácticas anteriores, necesitaríamos muchos para armar el circuito; y ciertamente no nos bastaría un solo proto-board. Puesto que no disponemos de ellos, hemos utilizado un circuito integrado que internamente tiene un juego de muchas compuestas lógicas, y que es reprogramable. El encapsulado dice así: ATMEL 0346 Δ ATF16V8B-15PC El código para programar este circuito lógico en particular lo pueden descargar pulsando aquí. Utilizamos el programa ATMEL WinCupl y un dispositivo programador. Los detalles de cómo programar uno de estos circuitos integrados, los veremos en otra entrada. |
 |
| Aquí está el circuito, una vez programado, puesto en su lugar en el proto-board. |
 |
| Conectamos las entradas a los pines respectivos. Ahorita todo está en ceros. Esto significa que el motor está apagado, por lo cual no hay inseguridad de nngún tipo y no debe sonar la alarma (un LED). Puesto que el circuito tiene 4096 combinaciones posibles de entradas, no es práctico hacerlas todas. A continuación vemos una muestra de unas pocas posibles combinaciones que muestran lo más importante del comportamiento del circuito: |
No comments:
Post a Comment